Adding and subtracting rational numbers

Here you will learn strategies on how to add and subtract rational numbers including using visual models, the number line, as well as using standard algorithms.

Students will first learn about integers in 6 th grade math as part of their work with the number system and expand that knowledge to operations with integers in the 7 th grade.

What are adding and subtracting rational numbers?

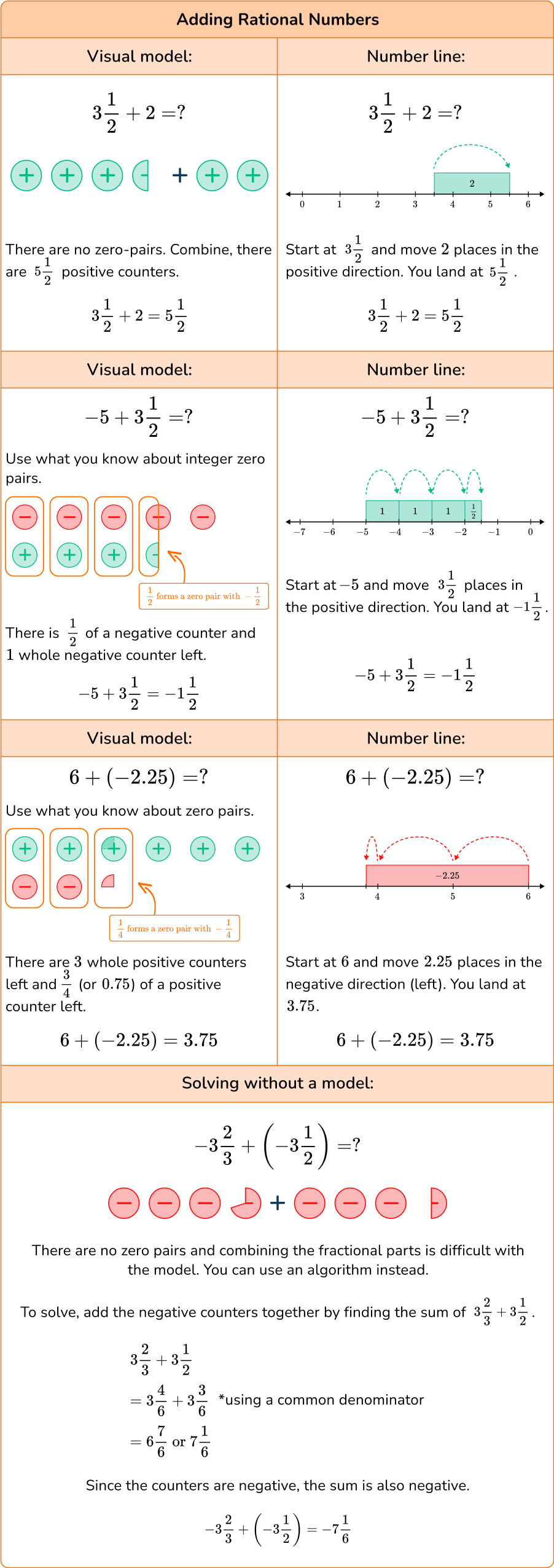
Adding and subtracting rational numbers is when you add or subtract two or more rational numbers together.

To add or subtract two rational numbers with the same denominator, we can add or subtract the numerators and write the result over the common denominator.

To add or subtract two rational numbers with different denominators, we must find a common denominator to add or subtract the numerators.

You can also add and subtract rational numbers using visual models or a number line.

What are adding and subtracting rational numbers?

Common Core State Standards

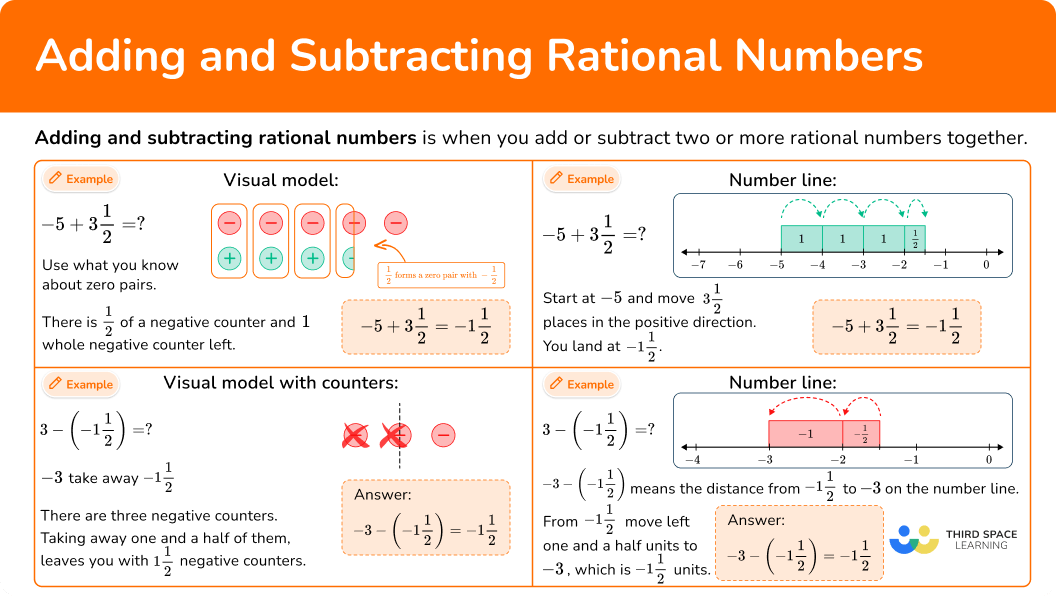
How does this apply to 7 th grade math?

• Grade 7: The Number System (7.NS.A.1)
  Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram.

• Grade 7: The Number System (7.NS.A.1a)
  Describe situations in which opposite quantities combine to make 0. For example, a hydrogen atom has 0 charge because its two constituents are oppositely charged.

• Grade 7: The Number System (7.NS.A.1d)
  Apply properties of operations as strategies to add and subtract rational numbers.

[FREE] Addition and Subtraction Check for Understanding (Grade 2 to 7)

Use this quiz to check your grade 2, 3, 4 and 7 students’ understanding of addition and subtraction. 15+ questions with answers covering a range of 2nd, 3rd, 4th and 7th grade addition and subtraction topics to identify areas of strength and support!

[FREE] Addition and Subtraction Check for Understanding (Grade 2 to 7)

Use this quiz to check your grade 2, 3, 4 and 7 students’ understanding of addition and subtraction. 15+ questions with answers covering a range of 2nd, 3rd, 4th and 7th grade addition and subtraction topics to identify areas of strength and support!

How to add and subtract rational numbers

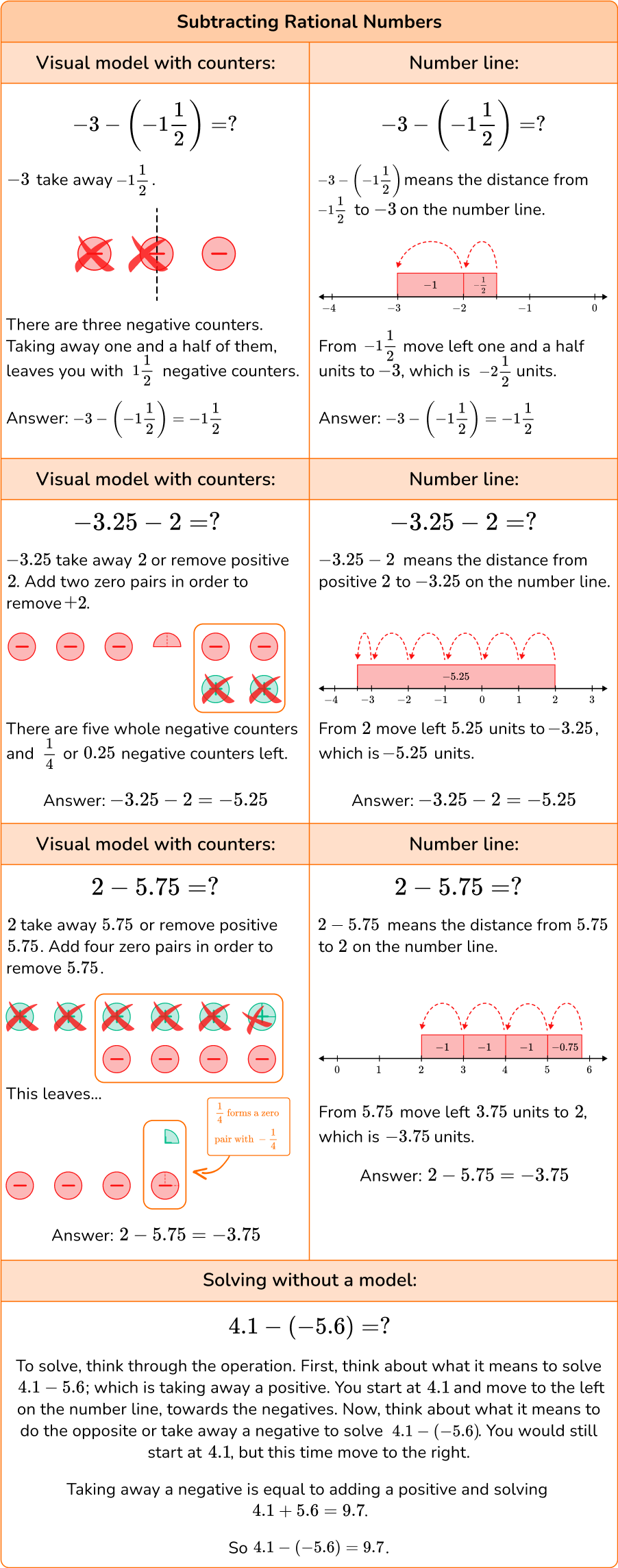
In order to add and subtract rational numbers using counters:

1. Model the problem with counters and use zero pairs when necessary.
2. The answer is the leftover counters.

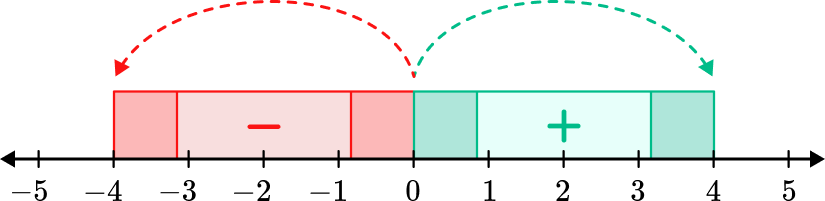
In order to add and subtract rational numbers using a number line:

1. To add, start at the first number and move to the second number; to subtract, start from the second number and move to the first number.
2. Write your answer.

Adding and subtracting rational numbers examples

Example 1: adding negative numbers using counters

1. Model the problem with counters and use zero pairs when necessary.

Use what you know about integer zero pairs.

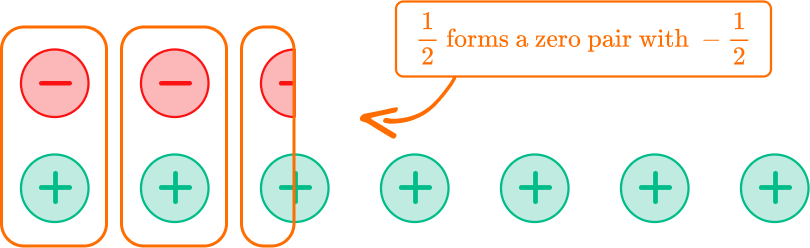
There is \cfrac of a positive counter and 4 whole positive counters left.

2 The answer is the leftover counters.

Example 2: subtracting a negative number using counters

Model the problem with counters and use zero pairs when necessary.

Model -4.5 with the counters.

There are not enough negatives to take away -6. Add 2 zero pairs in order to remove -6.

This leaves 2 positive counters and \cfrac of a negative counter.

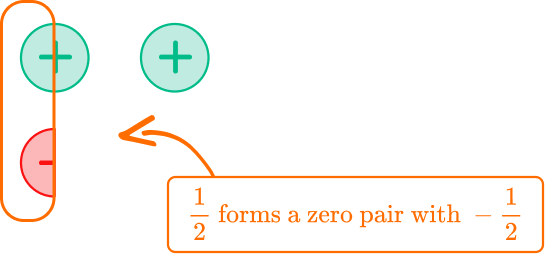
There is 1 positive counter left and \cfrac of a positive counter left.

The answer is the leftover counters.

Example 3: adding decimals with a number line

To add, start at the first number and move to the second number; to subtract, start from the second number and move to the first number.

-11.1 + (-0.3) is addition. Start at -11.1 and move in the negative direction (left) 0.3 places. You land at -11.4.

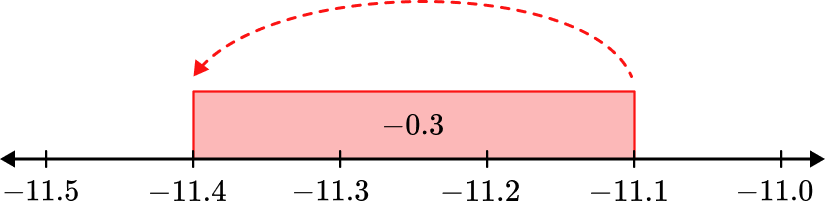
Write your answer.

How to add and subtract rational numbers with algorithms

In order to add and subtract rational numbers using algorithms:

1. Make sense of the calculation – relating to positive numbers when necessary.
2. Use an algorithm.
3. Decide if the final answer is positive or negative.

Example 4: subtracting fractions (mixed numbers) with different denominators

Make sense of the calculation – relating to positive numbers when necessary.

3 \, \cfrac-5 \, \cfrac \, is the distance from 5 \, \cfrac to 3 \, \cfrac \, .

5 \, \cfrac-3 \, \cfrac \, is the distance from 3 \, \cfrac to 5 \, \cfrac \, , which is the exact same part of the number line, just the opposite direction.

This means you can solve 5 \, \cfrac-3 \, \cfrac \, and use the opposite as the answer for 3 \, \cfrac-5 \, \cfrac \, .

Use an algorithm.

=\cfrac-\cfrac \hspace *Convert to improper fractions

=\cfrac-\cfrac \hspace *Subtract the numerators

=\cfrac which simplifies to 1 \, \cfrac

Decide if the final answer is positive or negative.

There are two ways to think about this…

Since for the distance on the number line you start at 5 \, \cfracand go back to 3 \, \cfrac, the direction is negative.

Example 5: adding negative decimals

Make sense of the calculation – relating to positive numbers when necessary.

-125.5 + (-34.56) combines two negative amounts, so the answer will be an even larger negative amount. You can combine like you would with positive numbers, to see what the total amount is.

Use an algorithm.

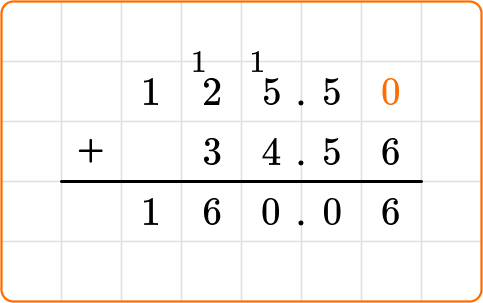
Decide if the final answer is positive or negative.

Adding two negative numbers results in a more negative number. For example, if you owe \$125.50 and then you make another purchase of \$34.56, now you owe even more. Your debt has grown, and debt is negative.

Example 6: adding a positive and negative decimal

Make sense of the calculation – relating to positive numbers when necessary.

125.5 + (-34.56) combines a positive and negative amount. Combining positive and negative creates 0 pairs, which has the same effect as subtracting two positive numbers. You can subtract like we would with positive numbers, to see what the total difference is.

Use an algorithm.

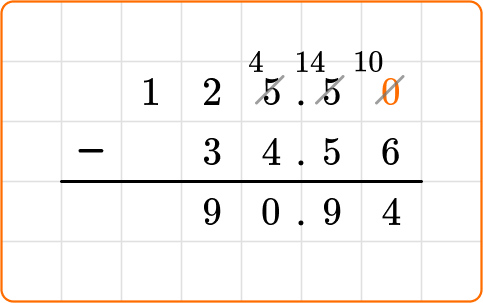
Decide if the final answer is positive or negative.

Now to decide if the answer is positive or negative, look at the original numbers being added. Since 125.5 is larger, the amount left over will also be positive.

125.5 + (-34.56) = 90.94

Teaching tips for adding and subtracting rational numbers

• Start with adding and subtracting rational expressions that involve only positive numbers. Students will use these skills to then operate with negative numbers. For students who are struggling to remember all algorithms, it may be necessary to provide them with step-by-step guides.

• When choosing worksheets, look for ones that include word problems. These types of problems give the rational numbers a real world context and allow students to practice figuring out which operation is appropriate.

Easy mistakes to make

• Getting the positive and negative direction on the number line backwards
  Right is positive and left is negative.

Confusing the different signs and rules
The rules for adding and subtracting integers can be used to solve with rational numbers. However, just like with integers it is important to think about why the rule works when using it, to avoid using the wrong rule.
For example,

-5 + 3 = \, ?
-5 + (-3) = -8

-5 + 3 = \, ?
5 + 3 = -2

Related addition and subtraction lessons

• Addition and subtraction
• Adding and subtracting negative numbers
• Add and subtract within 100
• Standard algorithm addition